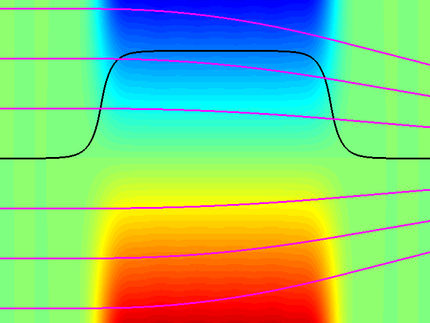
Schwingende Elektronenwolke mit Laser abgebildet
Physiker des Heidelberger Max-Planck-Instituts für Kernphysik haben mit ultraschnellen Laserblitzen die Elektronenbewegung in einem Atom abgelichtet. Untersucht wurde die Überlagerung zweier Quantenzustände in Argon-Ionen, die sich als schwingende Ladungswolke zeigt. In der Auswertung konnten sie ein direktes Abbild der zeitlichen Entwicklung einer Wellenfunktion mehrerer Elektronen gewinnen. Das Ergebnis zeigt eine gute Übereinstimmung mit Simulationsrechnungen und ist ein Test gängiger Modelle zur Tunnelionisation.
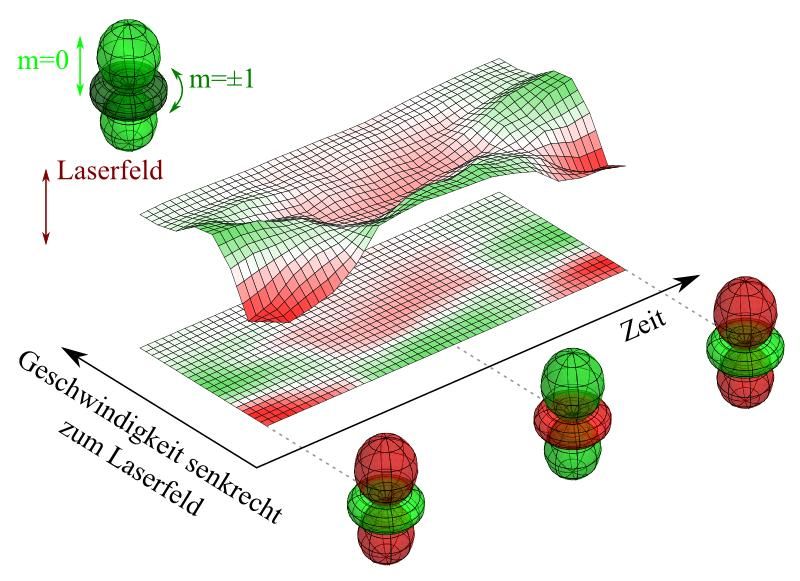
Wahrscheinlichkeitsverteilung der Elektronengeschwindigkeit senkrecht zum Laserfeld: dargestellt ist die Differenz der gemessenen zeitabhängigen Verteilung zur mittleren Verteilung (Farbfläche – rot: negative Abweichung, grün: positive Abweichung). Im Zustand m = 0 bewegt sich das Elektron vorzugsweise in Richtung des Laserfeldes – die Geschwindigkeiten senkrecht dazu fallen kleiner aus. Die Zustände m = ±1 können als ‚Kreisbewegung‘ in der Ebene senkrecht zum Laserfeld veranschaulicht werden – mit hier entsprechend größerer Geschwindigkeit. Pendelt das Elektron nun zwischen den beiden Zuständen, so beobachtet man abwechselnd in der Differenz ein Defizit bzw. einen Überschuss bei kleineren bzw. größeren Geschwindigkeiten.
MPIK
Es ist ein alter Wunschtraum vieler Physiker, die Bewegung eines Elektrons in einem Atom möglichst direkt zu vermessen. Dazu muss das Elektron aber aus seinem gebundenen Zustand befreit werden, z. B. durch Beschuss mit geladenen Teilchen (Elektronen oder Ionen) oder Licht. Die Schwierigkeit liegt darin, dass dabei die anfängliche Bewegung gestört wird und diese Störung nicht auf einfache Weise aus dem Messergebnis herausgerechnet werden kann. Gemäß einem Gedankenexperiment von Heisenberg könnte man die positive Ladung des Atomkerns ausschalten und das negativ geladene Elektron würde einfach mit der Geschwindigkeit, die es in diesem Moment hat, herausfliegen. Freilich müsste man dies vielfach wiederholen, da die Geschwindigkeit im Atom als Quantensystem nicht genau bestimmt ist. Das Ergebnis wäre dann die gesuchte statistische Geschwindigkeitsverteilung des Elektrons. Anschaulich würde eine Kugel, die in einer Schüssel umherkreist, dadurch befreit, dass man die Schlüssel schlagartig verschwinden lässt. Dies ist aber in der Realität genauso wenig möglich wie das Abschalten der Kernladung. Wohl aber kann man die Schüssel kippen und die Geschwindigkeit der herauslaufenden Kugel vermessen.
Analog geschieht genau das, wenn ein Atom dem starken elektrischen Feld eines intensiven Lasers ausgesetzt wird – das Elektron kann hier nicht nur über den Schüsselrand hinweglaufen, sondern sogar durch diesen hindurch ‚tunneln‘. Physiker aus der Gruppe um Robert Moshammer am Heidelberger Max-Planck-Institut für Kernphysik haben als besonders interessanten Anfangszustand die Überlagerung zweier Orbitale im Edelgas Argon betrachtet. Die Bindungsenergien in beiden Orbitalen sind ähnlich, sie haben aber eine unterschiedliche Ausrichtung im Raum. Charakterisiert sind sie durch die so genannte magnetische Quantenzahl m, welche hier die Werte -1, 0 oder +1 haben kann. Für m = 0 ist die Elektronenwolke hantelförmig entlang des Laserfeldes ausgerichtet, für m = ±1 dagegen reifenförmig in einer Ebene senkrecht dazu (Abbildung). Präpariert wird diese Überlagerung durch Tunnelionisation in einem ersten Laserimpuls, der genau ein Elektron entfernt – zurück bleibt daher eine Überlagerung zweier ‚Lochzustände‘.
Wird nun das so präparierte Ar+-Ion nach einer bestimmten Verzögerung von einem zweiten Laserimpuls getroffen, so kann eines der fünf verbleibenden Valenz-Elektronen entfernt werden. Diese verhalten sich komplementär zu dem Lochzustand und sind daher auch als eine solche Überlagerung beschreibbar. Misst man die Wahrscheinlichkeit, mit der ein Elektron im zweiten Laserimpuls freigesetzt wird, so schwankt sie periodisch mit der Verzögerungszeit. Dies entspricht genau dem quantenmechanischen Verhalten einer solchen Überlagerung, die zwischen den Orbitalen mit m = 0 und m = ±1 hin- und herpendelt. Für m = 0 ist das Elektron wegen der Ausrichtung des Orbitals parallel zum elektrischen Feld (der angreifenden Kraft) leichter zu ionisieren und es wird auch bevorzugt in diese Richtung freigesetzt. Die Geschwindigkeiten der Elektronen haben aber auch eine Komponente senkrecht (transversal) zum Laserfeld. Da in dieser Richtung der Laser keine Kraft ausübt, könnte man erwarten, damit einen direkten Zugang zur anfänglichen Geschwindigkeitsverteilung im gebundenen Zustand zu erhalten. Es sind aber zwei Störeffekte zu berücksichtigen: Erstens wird die Tunnelstrecke bei ‚schiefer‘ Durchdringung der Barriere etwas länger. Zweitens stört die stets vorhandene Anziehungskraft des Atomkerns die beobachtete Verteilung.
Um dieses Problem zu umgehen, haben die Forscher folgenden Trick angewandt: Sie bestimmten die Differenz der transversalen Geschwindigkeitsverteilung für einen bestimmten Zeitpunkt zur zeitgemittelten Verteilung. Als Zeitpunkte wählten sie jene, wo sich das Elektron überwiegend im Orbital mit m = 0 bzw. m = ±1 befindet. Im Zustand m = 0 bewegt sich das Elektron vorzugsweise in Richtung des Laserfeldes – die Geschwindigkeiten senkrecht dazu fallen kleiner aus. Die Zustände m = ±1 können als ‚Kreisbewegung‘ in der Ebene senkrecht zum Laserfeld veranschaulicht werden – mit hier entsprechend größerer Geschwindigkeit. Pendelt das Elektron nun zwischen den beiden Zuständen, so beobachtet man abwechselnd in der Differenz ein Defizit bzw. einen Überschuss bei kleineren bzw. größeren Geschwindigkeiten (Abbildung).
„Durch die Differenzbildung fallen die Störeffekte weitgehend heraus, da sie zeitunabhängig sind, während die zeitabhängige Schwingung der Elektronenwolke deutlich sichtbar bleibt“, erläutert Lutz Fechner, Doktorand in der Gruppe von Robert Moshammer. „Somit sind wir in der Lage, mit unseren Messungen gängige theoretische Modelle für die Tunnelionisation zu testen. Wir waren sogar überrascht, wie gut die Übereinstimmung mit einem einfachen theoretischen Modell ist, welches die Störung durch die Kernladung gar nicht berücksichtigt.“ Von zukünftigen Experimenten erwarten die Forscher detaillierte Informationen über den Ionisationsprozess in starken Laserfeldern und über die Dynamik mehrerer gebundener Elektronen.