Ein Blick in die vierte Dimension
In unserer alltäglichen Erfahrung hat der Raum drei Dimensionen. Vor kurzem konnte jedoch in Experimenten ein physikalisches Phänomen beobachtet werden, das nur in vier Raumdimensionen vorkommt. Die theoretischen Grundlagen dazu hat ein ETH-Forscher entwickelt.
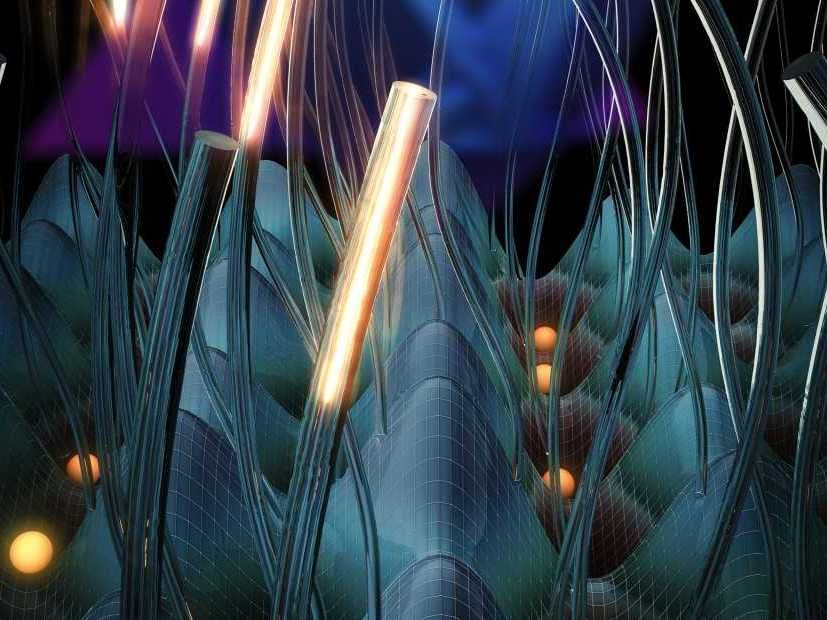
Ein physikalisches Phänomen in vier Raumdimensionen wurde in zwei Experimenten realisiert: mit Licht in Wellenleitern (geschlängelte Röhren) und mit kalten Atomen (orange Kugeln) in optischen Gittern.
ETH Zürich
Unter «vierter Dimension» versteht man für gewöhnlich die Zeit, seit Albert Einstein 1905 in Zürich die spezielle Relativitätstheorie entwickelte. Wie aber kann man sich eine vierte räumliche Dimension – zusätzlich zu oben-unten, rechts-links, vorne-hinten – vorstellen?
In der Kunst hat das zum Beispiel Salvador Dalí versucht: Seine 1954 gemalte Kreuzigungsszene zeigt ein Kruzifix, das aus der dreidimensionalen Auffaltung eines Hyperkubus in vier Dimensionen besteht (ähnlich der Auffaltung eines Würfels in Quadrate).
Einen ganz anderen, aber nicht weniger faszinierenden Einblick in die vierte Raumdimension haben nun zwei Teams von Wissenschaftlern aus der Schweiz, USA, Deutschland, Italien und Israel gewonnen. In beiden Arbeiten, die kürzlich im Fachmagazin Nature erschienen sind, spielte der ETH-Forscher Oded Zilberberg, Professor am Institut für theoretische Physik, eine zentrale Rolle. Er schuf die theoretischen Grundlagen für die Experimente, in denen ein vierdimensionales physikalisches Phänomen in zwei Dimensionen beobachtet werden konnte.
Der Quanten-Hall-Effekt
In beiden Experimenten ging es um den so genannten Quanten-Hall-Effekt. Üblicherweise tritt dieser Effekt in Grenzflächen zwischen zweit Materialien auf, in denen Elektronen sich nur in zwei Dimensionen bewegen können. Ein senkrecht zum Material stehendes Magnetfeld führt dann zum klassischen Hall-Effekt. Fliesst ein Strom durch das Material, so entsteht senkrecht zur Stromrichtung eine elektrische Spannung – je grösser das Magnetfeld, desto höher die Spannung. Das liegt daran, dass das Magnetfeld eine Kraft erzeugt, die im rechten Winkel zur Bewegungsrichtung wirkt (die Lorentzkraft) und die Elektronen ablenkt.
Bei sehr niedrigen Temperaturen und sehr starken Magnetfeldern kommt allerdings die Quantenmechanik zum Tragen, so dass die Spannung nicht mehr kontinuierlich, sondern in diskreten Stufen ansteigt. Drei Physik-Nobelpreise sind bislang für experimentelle und theoretische Arbeiten zum Quanten Hall Effekt vergeben worden.
Eine Frage der Topologie
Der Quanten-Hall-Effekt lässt sich auch als topologisches Phänomen verstehen. Die Topologie beschreibt beispielsweise, wie viele «Löcher» ein Objekt hat und in welche anderen Formen es sich ohne Zerschneiden umwandeln lässt. Ähnliche Gesetze führen beim Quanten-Hall-Effekt dazu, dass die Elektronen sich nur auf topologisch genau bestimmten Bahnen bewegen können. Für bestimmte Stärken des Magnetfelds etwa kann der elektrische Strom nur an den Rändern des Materials, nicht aber in seinem Inneren fliessen.
Vor etwa zwanzig Jahren wurde mathematisch gezeigt, dass es entsprechende topologische Effekte auch in vier räumlichen Dimensionen geben sollte. «Das war damals aber eher Science-Fiction», sagt Oded Zilberberg, «denn so etwas in Experimenten tatsächlich zu beobachten, schien unmöglich – der physikalische Raum hat nun einmal nur drei Dimensionen. »
Virtuelle Dimensionen durch topologisches Pumpen
Doch Zilberberg hatte eine clevere Idee: Mit Hilfe von so genannten topologischen Pumpen sollte es möglich sein, den beiden realen Dimensionen des Quanten-Hall-Effekts noch jeweils eine virtuelle Dimension hinzuzufügen. Eine topologische Pumpe funktioniert dadurch, dass eine bestimmte Kontrollgrösse des physikalischen Systems moduliert wird, wodurch sich sein Quantenzustand im Laufe der Zeit auf charakteristische Weise ändert. Das Endresultat sieht dann so aus, als habe sich das System in einer zusätzlichen Raumdimension bewegt. Auf diese Weise kann man theoretisch ein zweidimensionales System in ein vierdimensionales verwandeln.
Ein optisches Abbild der vierten Dimension
Dass dies auch in der Praxis funktioniert, haben Wissenschaftler nun in zwei unabhängigen Experimenten gezeigt. Physiker um Mikael Rechtsman an der Penn State University in den USA verwirklichten Oded Zilberbergs Idee gemeinsam mit der Forschungsgruppe von Kevin Chen an der University of Pittsburgh, indem sie mit Laserstrahlen ein zweidimensionales Gitter aus Wellenleitern in einen fünfzehn Zentimeter langen Glasblock brannten. Diese Wellenleiter waren allerdings nicht geradlinig, sondern wanden sich schlangenförmig durch das Glas, so dass die Abstände zwischen ihnen sich entlang des Glasblocks änderten. Lichtwellen, die sich durch die Wellenleiter bewegten, konnten so je nach Abstand mehr oder weniger leicht in einen benachbarten Wellenleiter überspringen.
Diese sich stetig verändernden Kopplungen zwischen den Wellenleitern wirkten als topologische Pumpen und verdoppelten so die Anzahl der Dimensionen des Experiments von zwei auf vier. Den erwarteten vierdimensionalen Quanten-Hall-Effekt konnten die Forscher nun buchstäblich «sehen», indem sie auf einer Seite des Glasblocks Licht in die Wellenleiter speisten und mit einer Videokamera aufnahmen, was auf der anderen Seite herauskam. So wurden zum Beispiel die für den vierdimensionalen Quanten-Hall-Effekt charakteristischen Randzustände, in denen nur aus den Wellenleitern am Rand des Gitters Licht austreten sollte, direkt sichtbar.
Vierdimensionaler quantisierter Transport von kalten Atomen
Mit Hilfe von extrem kalten Atomen, die in optischen Gittern aus gekreuzten Laserstrahlen gefangen sind, realisierten Immanuel Bloch und seine Mitarbeiter am Max-Planck-Institut für Quantenoptik in München ebenfalls topologische Pumpen. In ihrem Experiment wurde das Pumpen dadurch erreicht, dass die Eigenschaften der gespaltenen Gittertöpfe, in denen die Atome eingefangen waren, periodisch verändert wurden.
Durch Messungen der zweidimensionalen Bewegung der Atome in dem Gitter konnten sie bestätigen, dass sich diese gemäss dem Quanten-Hall-Effekt in vier Dimensionen verhielten. Insbesondere konnten sie direkt die quantisierten Transportphänomene beobachten, die für diesen Fall vorhergesagt worden waren (und die der senkrecht zur Stromrichtung entstehenden Spannung im gewöhnlichen, zweidimensionalen Quanten-Hall-Effekt entsprechen).
Fortschritt in der Grundlagenforschung
Der praktische Nutzen des Ganzen? «Im Moment sind diese Experimente noch meilenweit von nützlichen Anwendungen entfernt», gibt Zilberberg zu. Doch für die Grundlagenforschung stellen sie einen wichtigen Fortschritt dar. Physiker können jetzt nicht nur auf dem Papier, sondern auch experimentell untersuchen, welche Auswirkungen Phänomene aus vier (oder sogar noch mehr) Dimensionen in unserer alltäglichen dreidimensionalen Welt haben können.
Ein Beispiel dafür sind Quasikristalle in Metalllegierungen. In drei Raumdimensionen habe diese zwar keine periodische Struktur, doch sieht man sie sich in virtuellen höheren Dimensionen an, so weisen sie wieder regelmässige Muster auf. Und schliesslich ist da noch die Stringtheorie, gemäss der höhere Raumdimensionen derart «kompaktifiziert» sein sollen, dass am Ende unsere normale dreidimensionale Welt entsteht.
Originalveröffentlichung
Lohse M, Schweizer C, Price HM, Zilberberg O, Bloch I.; "Exploring 4D quantum Hall physics with a 2D topological charge pump"; Nature 553, 55–58 (04 January 2018).
Zilberberg O, Huang S, Guglielmon J, Wang M, Chen KP, Kraus YE, Rechtsman MC; "Photonic topological boundary pumping as a probe of 4D quantum Hall physics"; Nature 553, 59–62 (04 January 2018).
Weitere News aus dem Ressort Wissenschaft
![[Fe]-Hydrogenase-Katalyse mittels Parawasserstoff-verstärkter Kernmagnetresonanzspektroskopie sichtbar gemacht](https://img.chemie.de/Portal/News/675fd46b9b54f_sBuG8s4sS.png?tr=w-712,h-534,cm-extract,x-0,y-16:n-xl)
Diese Produkte könnten Sie interessieren
Rotating Ring Disk Elektrode Rotator von C3 Prozess- und Analysentechnik
Präzise Rotation und einfacher Elektrodenwechsel - Entdecken Sie das innovative Rotator-System!
Elektrochemische Messzellen und Elektroden von C3 Prozess- und Analysentechnik
Ersetzen Sie viele Messzellen mit unserer vielseitigen Voltammetriezelle für präzise Messergebnisse
Interface 1010 von C3 Prozess- und Analysentechnik
Optimieren Sie Ihre elektrochemische Messungen für präzise Ergebnisse und vielfältige Anwendungsmöglichkeiten
Reference 620 von C3 Prozess- und Analysentechnik
Potentiostat / Galvanostat / ZRA mit maximaler Empfindlichkeit und minimalem Rauschen für wegweisende Forschung
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
