Versteckte Ordnung in der Unordnung
Annäherung an Hyperuniformität in amorphen Systemen lässt sich zur Entwicklung neuartiger Materialien und Erforschung von Zellgewebe nutzen
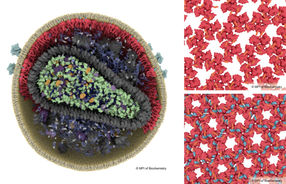
Den Raum in Zellen mit optimalen geometrischen Eigenschaften einzuteilen, ist eine zentrale Herausforderung in vielen Bereichen der Wissenschaft und Technik. Nun haben Forscher am Karlsruher Institut für Technologie (KIT) mit Kollegen aus mehreren Ländern festgestellt, dass bei amorphen, das heißt ungeordneten Systemen eine Optimierung der einzelnen Zellen schrittweise zur stets gleichen Struktur führt, obwohl diese amorph bleibt. Dabei nähert sich die ungeordnete Struktur rasch einer Hyperuniformität an – einer versteckten Ordnung in großen Maßstäben.
Wie ungeordnet ein System anfangs auch sein mag – wird jede Zelle einzeln optimiert, bildet sich Schritt für Schritt stets die gleiche Struktur mit einer versteckten Ordnung.
Michael A. Klatt
Von der Suche nach dem optimalen Schaum bis zur Suche nach einer möglichst platzsparenden Art, Kugeln zusammenzupacken – die ideale Tesselierung des dreidimensionalen Raums, das heißt seine lückenlose Unterteilung in Zellen mit speziellen geometrischen Eigenschaften, beschäftigt die Wissenschaft schon lange. Sie ist nicht nur theoretisch interessant, sondern für viele praktische Anwendungen relevant, unter anderem in der Telekommunikation, zur Bildverarbeitung oder für komplexe Granulate. Mit einem speziellen Problem der Tesselierung, nämlich dem Quantisierungsproblem, haben sich nun Forscher am Institut für Stochastik des KIT genauer befasst. „Ziel ist eine Einteilung des Raums in Zellen, bei der – intuitiv gesagt – alle Punkte in einer Zelle so nahe wie möglich am Zellzentrum liegen“, erklärt Dr. Michael Andreas Klatt, früherer Mitarbeiter des Instituts, der jetzt an der Princeton University in den USA tätig ist. Lösungen des Quantisierungsproblems lassen sich zur Entwicklung neuartiger Materialien nutzen und können künftig auch zu einem besseren Verständnis der einzigartigen Eigenschaften von komplexem Zellgewebe beitragen.
In ihrer nun in der Zeitschrift Nature Communications veröffentlichten theoretischen Arbeit, die Methoden der stochastischen Geometrie und der statistischen Physik verbindet, verwendeten die Forscher am KIT sowie an der Princeton University, an der Friedrich-Alexander-Universität (FAU) Erlangen-Nürnberg, am Ruđer Bošković Institut in Zagreb und an der Murdoch University in Perth den sogenannten Lloyd-Algorithmus, eine Methode zur Einteilung des Raums in gleichmäßige Regionen. Jede Region weist genau ein Zentrum auf und umfasst diejenigen Punkte des Raums, die näher an diesem Zentrum liegen als an jedem anderen Zentrum. Solche Regionen heißen Voronoi-Zellen. Aus allen Punkten, die mehr als ein nächstgelegenes Zentrum besitzen, also die Grenzen der Regionen bilden, entsteht das Voronoi-Diagramm.
Die Wissenschaftler untersuchten die schrittweise lokale Optimierung verschiedenster Punktmuster und stellten fest, dass alle vollständig amorphen, das heißt ungeordneten Zustände nicht nur vollständig amorph bleiben, sondern dass die anfangs vielfältigen Prozesse zu einem statistisch ununterscheidbaren universellen Ensemble konvergieren. Dabei gleicht die schrittweise lokale Optimierung auch extreme globale Schwankungen der Dichte schnell aus. „So entsteht eine Struktur, die fast hyperuniform ist – sie zeigt keine offensichtliche Ordnung, wohl aber eine versteckte Ordnung in großen Maßstäben“, berichtet Klatt.
Somit ist diese versteckte Ordnung in den amorphen Systemen universell, das heißt stabil und unabhängig von den Eigenschaften des Ausgangszustands. Das vermittelt grundlegende Einsichten in das Wechselspiel von Ordnung und Unordnung. Praktisch nutzen lässt sich dies unter anderem zur Entwicklung neuartiger Materialien: Interessant sind beispielsweise photonische Metamaterialien, ähnlich einem Halbleiter für Licht, oder sogenannte Blockcopolymere, das heißt Nanopartikel, die aus längeren Sequenzen oder Blöcken verschiedenartiger Moleküle zusammengesetzt sind und selbstorganisiert regelmäßige und komplexe Strukturen ausbilden.
Originalveröffentlichung
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
