Magische Verdrehungswinkel von Graphenblättern identifiziert
Graphen ist 200 Mal stärker als Stahl und kann bis zu 6 Mal leichter sein. Allein diese Eigenschaften machen es zu einem beliebten Material bei der Herstellung. Forscher an der University of Illinois at Urbana-Champaign haben kürzlich weitere Eigenschaften von Graphenplatten entdeckt, die der Industrie zugute kommen können.
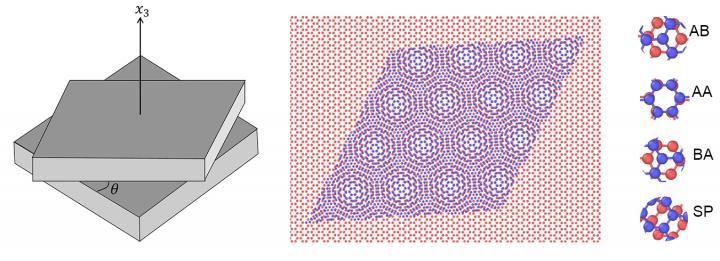
Atomistische Konfiguration von verdrilltem Zweischichtgraphen
Department of Aerospace Engineering, Grainger Engineering
Der Doktorand Soumendu Bagchi hat zusammen mit seinem Berater Huck Beng Chew von der Abteilung für Luft- und Raumfahrttechnik in Zusammenarbeit mit Harley Johnson von der Abteilung für Maschinenbau und Ingenieurwesen ermittelt, wie sich verdrehte Graphenplatten verhalten und wie stabil sie bei verschiedenen Größen und Temperaturen sind.
"Wir haben uns auf zwei übereinander gestapelte Graphenplatten konzentriert, aber mit einem Verdrehwinkel", sagte Bagchi. "Wir haben atomistische Simulationen bei verschiedenen Temperaturen für verschiedene Größen von Graphenplatten durchgeführt. Mit den Erkenntnissen aus diesen Simulationen haben wir ein analytisches Modell entwickelt - man kann jede beliebige Plattengröße und jeden beliebigen Verdrehungswinkel einstecken, und das Modell sagt die Anzahl der lokalen stabilen Zustände sowie die kritische Temperatur voraus, die erforderlich ist, um jeden dieser Zustände zu erreichen.
Bagchi erklärte, dass zweischichtiges Graphen in einer unverdrehten Bernal-Stapelkonfiguration existiert, was auch die wiederholte Stapelfolge von kristallinem hexagonalem Graphit ist. Wenn zweischichtiges Graphen verdreht wird, möchte es sich wieder in seinen ursprünglichen Zustand aufdrehen, weil dies der stabilste Zustand und die stabilste Anordnung der Atome ist.
"Wenn die verdrillte Atomstruktur erhitzt wird, neigt sie dazu, zurückzudrehen, aber es gibt bestimmte magische Verdrehungswinkel, bei denen die Struktur unter einer bestimmten Temperatur stabil bleibt. Und es gibt auch eine Größenabhängigkeit. Das Spannende an unserer Arbeit ist, dass wir abhängig von der Größe der Graphenfolie vorhersagen können, wie viele stabile Zustände man haben wird, die magischen Verdrehungswinkel bei diesen stabilen Zuständen sowie den Temperaturbereich, den das verdrillte Graphen benötigt, um von einem stabilen Zustand in einen anderen überzugehen", sagte Bagchi.
Laut Chew haben Hersteller versucht, Graphen-Transistoren herzustellen, und verdrillte Graphen-Doppelschichten sind dafür bekannt, dass sie aufregende elektronische Eigenschaften aufweisen. Bei der Herstellung dieser Graphen-Transistoren ist es wichtig zu wissen, bei welcher Temperatur das Material angeregt wird, um eine bestimmte Rotation oder mechanische Reaktion zu erreichen.
"Sie wussten, dass ein Graphenblatt bestimmte elektronische Eigenschaften hat, und wenn man ein zweites Blatt in einem Winkel hinzufügt, erhält man neue einzigartige Eigenschaften. Aber eine einzelne Atomlage ist nicht leicht zu manipulieren. Im Wesentlichen beantwortet diese Studie Fragen darüber, wie sich verdrehte Graphenplatten unter thermischer Belastung verhalten, und gibt Einblicke in die Selbstausrichtungsmechanismen und -kräfte auf atomarer Ebene. Dies könnte den Herstellern den Weg zur Feinsteuerung des Verdrehungswinkels von 2D-Materialstrukturen ebnen. Sie können Parameter direkt in das Modell einfließen lassen, um die notwendigen Bedingungen zu verstehen, die zum Erreichen eines bestimmten Verdrehungszustandes erforderlich sind.
Bagchi sagte, niemand habe die 2D-Eigenschaften solcher Materialien untersucht. Es handelt sich um eine sehr grundlegende Studie, die als ein anderes Projekt begann, als er auf etwas Ungewöhnliches stieß.
"Er bemerkte, dass die Graphenblätter eine gewisse Temperaturabhängigkeit zeigten", sagte Chew. "Wir fragten uns, warum es sich so verhält - nicht wie ein normales Material.
"Bei normalen Materialien ist die Grenzfläche normalerweise sehr stark. Bei Graphen ist die Grenzfläche sehr schwach, so dass die Schichten gleiten und sich drehen können. Die Beobachtung dieser interessanten Temperaturabhängigkeit war nicht geplant. Das ist die Schönheit der Entdeckung in der Wissenschaft."
Hinweis: Dieser Artikel wurde mit einem Computersystem ohne menschlichen Eingriff übersetzt. LUMITOS bietet diese automatischen Übersetzungen an, um eine größere Bandbreite an aktuellen Nachrichten zu präsentieren. Da dieser Artikel mit automatischer Übersetzung übersetzt wurde, ist es möglich, dass er Fehler im Vokabular, in der Syntax oder in der Grammatik enthält. Den ursprünglichen Artikel in Englisch finden Sie hier.
Originalveröffentlichung
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
