Ein Rätsel der Kristallform ist endlich gelöst
Die Methode kann die Form von Kristallen vorhersagen, denen es an Symmetrie fehlt
Die Form eines Kristalls wird durch die ihm innewohnende Chemie bestimmt, eine Eigenschaft, die letztlich seine endgültige Form bis ins kleinste Detail bestimmt. Aber manchmal macht das Fehlen von Symmetrie in einem Kristall die Oberflächenenergien seiner Facetten unbestimmbar, was jede theoretische Vorhersage seiner Form verwirrt.
Symbolbild
Computer-generated image
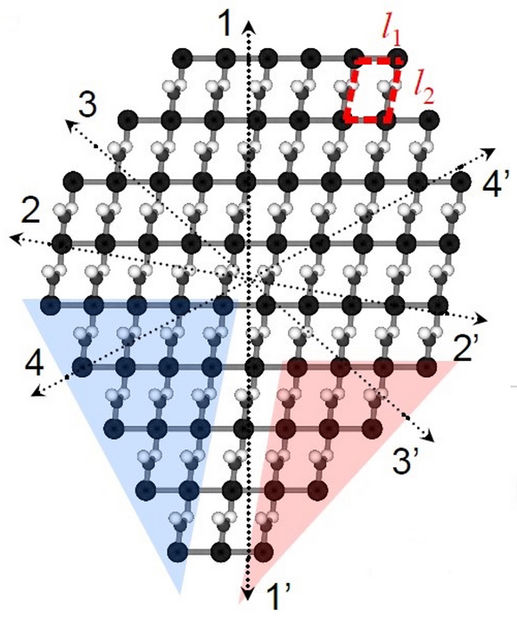
Forscher der Rice University haben eine Methode entwickelt, mit der sich vorhersagen lässt, wie Kristalle aufgrund ihrer inneren Chemie ihre Form annehmen, selbst wenn der Kristall keine Symmetrie aufweist. Diese Darstellung eines Silbernitratkristalls hat acht Kanten, von denen keine zu den anderen passt. Der Algorithmus des Rice-Teams war dennoch in der Lage, seine Form vorherzusagen.
Illustration by Luqing Wang/Rice University
Theoretiker der Rice University wollen einen Weg gefunden haben, dieses Rätsel zu umgehen, indem sie den Oberflächen oder - im Falle von zweidimensionalen Materialien - den Kanten beliebige latente Energien zuweisen.
Ja, es scheint wie Betrug, aber so wie ein Zauberer eine bestimmte Karte in einem Kartenspiel findet, indem er die Möglichkeiten einschränkt, kann ein kleiner algebraischer Taschenspielertrick das Problem der Vorhersage der Form eines Kristalls sehr gut lösen.
Die in Nature Computational Science beschriebene Methode zeigt, dass die Verwendung von so genannten Hilfskantenenergien die Vorhersagen wieder in Einklang mit der Wulff-Konstruktion bringen kann, einem geometrischen Rezept, das seit mehr als einem Jahrhundert verwendet wird, um zu bestimmen, wie Kristalle zu ihrer endgültigen Gleichgewichtsform gelangen.
Die frei zugängliche Arbeit des Materialphysikers Boris Yakobson, des Hauptautors und Absolventen Luqing Wang und ihrer Kollegen an der George R. Brown School of Engineering von Rice stellt Algorithmen vor, die beliebige Zahlen für die Faktoren auf der rechten Seite der Gleichungen verwenden und dennoch die richtige, einzigartige Formlösung liefern.
"Die Frage der Form ist zwingend, aber Forscher haben jahrelang versucht, Oberflächenenergien für asymmetrische Kristalle zu berechnen, und sind dabei gescheitert", sagte Yakobson. "Es stellte sich heraus, dass wir in ein Kaninchenloch fielen, aber wir wussten, dass, wenn die Natur eine Lösung durch eine Trillion atomarer Bewegungen finden kann, es auch einen Weg für uns geben sollte, sie zu bestimmen."
Er sagte, dass das wachsende Interesse an 2D-Materialien in letzter Zeit die neue Studie motiviert hat. "Wir hatten einen 'Heureka'-Moment: Nachdem wir unser geometrisches Denken auf algebraisch umgestellt hatten, fügten wir Schließungsgleichungen hinzu, die beliebige Parameter enthalten", sagte Yakobson. "Diese scheinen nutzlos zu sein, aber wir haben alles durch den Computer laufen lassen und beobachtet, dass eine wohldefinierte Form herauskam", sagte er.
"Der schwierige Teil war, unsere Gutachter davon zu überzeugen, dass die Kantenenergie wirklich undefinierbar ist, aber eine Lösung kann trotzdem erreicht werden", sagte Wang.
Die Arbeit könnte Forschern, die Kristalle für katalytische, lichtemittierende, sensorische, magnetische und plasmonische Anwendungen von unten nach oben züchten, ein wertvolles Werkzeug an die Hand geben, insbesondere wenn ihre Form und ihre aktiven Kanten von besonderer Bedeutung sind.
Die Forscher wiesen darauf hin, dass natürliche Kristalle den Luxus der geologischen Zeit genießen. Sie erreichen ihre Form durch ein "unerbittliches Versuch-und-Irrtum-Experiment" auf der Suche nach dem Gleichgewicht, also der minimalen Energie aller Atome, aus denen sie bestehen.
Aber rechnerische und theoretische Ansätze können einfach nicht mit Milliarden von Atomen auf einmal umgehen, daher stützen sie sich im Allgemeinen auf die Energien der nach außen gerichteten Atome. Für viele Kristalle, die gleichwertige Facetten oder Kanten haben, funktioniert das ganz gut.
In 2D-Materialien sind im Wesentlichen alle Atome "nach außen gerichtet". Wenn ihre Kanten durch Symmetrie äquivalent sind - z. B. bei Rechtecken - ist die Vervollständigung einer Wulff-Konstruktion einfach, nachdem man die Kantenenergien über die Dichtefunktionaltheorie berechnet hat.
Aber wenn keine Symmetrie vorliegt, wenn alle Kanten unterschiedlich sind, ist die berechnete durchschnittliche Energie bedeutungslos, so Yakobson.
"Die Natur hat die Antwort, um einen Kristall zu formen, unabhängig davon, was sie über die Kantenenergien 'weiß' oder nicht weiß", sagte er. "Es gibt also eine Antwort. Unsere Herausforderung bestand darin, sie mit der Theorie nachzuahmen."
Der erste Schritt zur Lösung bestand darin, bewusst auf die Suche nach den unbekannten absoluten Kantenenergien zu verzichten und sich stattdessen mit ihren wohldefinierten berechenbaren Kombinationen zu beschäftigen, so Yakobson. Geometrisch gesehen war dies ein ziemliches Rätsel, und für asymmetrische Massenmaterialien war es hoffnungslos kompliziert.
"Aber 2D-Materialien und ihre ebenen Polygone machten die Lösung des Problems einfacher, als sich mit vielschichtigen Polyedern auseinandersetzen zu müssen", sagte er.
Die Ermittlung und Festlegung von Durchschnittsenergien war nur der erste Schritt, gefolgt von "Schließungsgleichungen", die eine beliebige latente Materialenergie für die rechte Seite der Gleichung verwendeten. Selbst wenn die letztgenannten Zahlen absichtlich falsch waren, ergab die Anwendung auf die lehrbuchmäßige Wulff-Konstruktion die richtige Kristallform.
Die Gruppe testete ihre Theorie an mehreren 2D-Kristallen und verglich die Ergebnisse mit den beobachteten Endformen der Kristalle. Ihre vielseitigen Gleichungen sagten erfolgreich die experimentell nachgewiesenen Formen des abgestumpften Rechtecks von 2D-Zinnselenid, einem vielversprechenden thermo- und piezoelektrischen Material, und der asymmetrischen Nadeln von Silbernitrit voraus.
Hinweis: Dieser Artikel wurde mit einem Computersystem ohne menschlichen Eingriff übersetzt. LUMITOS bietet diese automatischen Übersetzungen an, um eine größere Bandbreite an aktuellen Nachrichten zu präsentieren. Da dieser Artikel mit automatischer Übersetzung übersetzt wurde, ist es möglich, dass er Fehler im Vokabular, in der Syntax oder in der Grammatik enthält. Den ursprünglichen Artikel in Englisch finden Sie hier.
Originalveröffentlichung
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
