Effiziente Suche nach verbesserten Energie-Materialien mit Hilfe von künstlicher Intelligenz
Solche Materialien können dazu beitragen, die anhaltende Energiekrise zu lindern
Wissenschaftler des NOMAD Laboratory am Fritz-Haber-Institut der Max-Planck-Gesellschaft haben kürzlich einen auf künstlicher Intelligenz (KI) basierenden Ansatz vorgeschlagen, mit der sich die Suche nach neuartigen Materialien mit verbesserten Eigenschaften dramatisch beschleunigen lässt. Die Vorteile dieser Strategie wurden durch die Identifikation von mehr als 50 stark wärmeisolierenden Materialien demonstriert. Solche Materialien können dazu beitragen, die anhaltende Energiekrise zu lindern. Diese sind nämlich die Grundlage für die Entwicklung effizienter thermoelektrischer Elemente, die ungenutzte Abwärme in nutzbaren elektrischen Strom umwandeln.
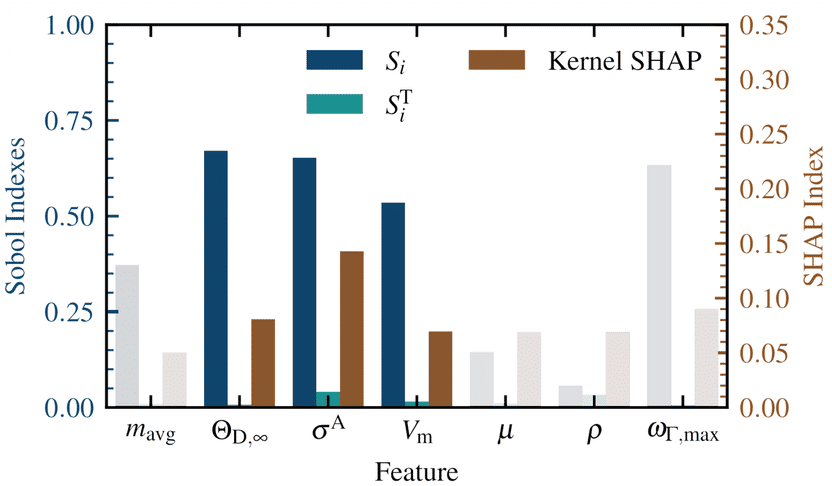
Figur 1 Die Sobol-Indizes Si und SiT sowie die Kernel-SHAP-Werte für jede Eigenschaft im Modell. Diese Werte sind alle Metriken für die Bedeutung von Eigenschaften, wobei 0 bedeutet, dass die Eigenschaft keine Auswirkung hat, und ein größerer Wert darauf hindeutet, dass die Eigenschaft wichtiger ist.
© Thomas Purcell
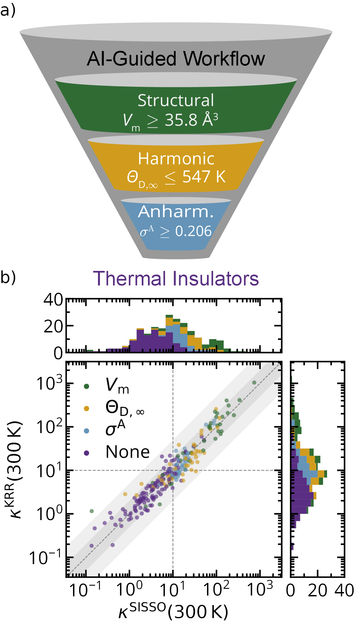
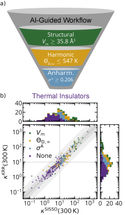
Figur 2 a) Schematische Darstellung des Hochdurchsatz-Arbeitsablaufs, der zur Suche nach neuen Wärmedämmstoffen verwendet wird. b) Ein Streudiagramm zeigt die vorhergesagte Wärmeleitfähigkeit für 227 thermodynamisch stabile elektrische Isolatoren sowohl aus einem SISSO- als auch aus einem Kernel-Ridge-Regression (KRR)-Modell. Die Farbe entspricht den in Teil a) beschriebenen fehlgeschlagenen Tests.
© Thomas Purcell
Da heutzutage mehr als 40% der weltweit genutzten Energie als Abwärme verpufft, ist die Entdeckung neuer und verbesserter thermoelektrischer Materialien von entscheidender Bedeutung, um wachsenden Herausforderungen des Klimawandels entgegenzuwirken. Eine Möglichkeit, die thermoelektrische Effizienz eines Materials zu erhöhen, besteht darin, seine Wärmeleitfähigkeit, κ, zu reduzieren und somit das für den thermoelektrischen Effekt benötigte Temperaturgefälle aufrechtzuerhalten. Da aber sowohl die experimentelle als auch die rechnerische Bestimmung von κ kosten- und arbeitsintensiv ist, beschränkten sich bisherige Untersuchungen von κ auf nur eine verschwindend kleine Auswahl von Materialien. Mit dem von den NOMAD Forschern entwickelten KI-Ansatz lassen sich Materialien hierarchisch aussortieren, so dass die Kosten reduziert bzw. bei gleichbleibenden Aufwand viel mehr Materialien untersucht werden können.
Die kürzlich in npj Computational Materials veröffentlichte Arbeit schlägt eine neue Methode vor, wie sich mit Hilfe von künstlicher Intelligenz (KI) die Suche nach neuen Materialien automatisieren und gezielt steuern lassen kann. Dabei werden Materialien nicht, wie sonst üblich, anhand von physikalischer oder chemischer Intuition du bekannten oder vermuteten Trends ausgewählt oder aussortiert. Stattdessen nutzt das neue Verfahren fortschrittliche KI-Methoden, um aus vorhandenen Daten die Bedingungen zu lernen, die zum gewünschten Ergebnis führen. Diese Arbeit hat daher das Potenzial, die Suche nach neuen Materialien mit Hilfe von quantitativen Vorhersagen zu beschleunigen.
Der erste Schritt bei diesem neuartigen Ansatz besteht darin, fortgeschrittene statistische KI-Methoden zu verwenden, um die gewünschte Eigenschaft – in diesem Fall κ – zu modellieren. Zu diesem Zweck wird die "Sure-Independence Screening and Sparsifying Operator" (SISSO) Methode verwendet, die die grundlegenden Abhängigkeiten zwischen verschiedenen Materialeigenschaften aus einer Vielzahl möglicher Zusammenhänge enthüllt. Dabei ist dieser Ansatz im Vergleich zu anderen "Black-Box" KI-Modellen ähnlich genau, liefert aber zusätzlich noch analytische Beziehungen zwischen verschiedenen Materialeigenschaften. Dies ermöglicht es dann auch, mit modernen mathematischen Metriken herauszufinden, welche Materialeigenschaften unter welchen Umständen für welche Zieleigenschaft am einflussreichsten sind. Im Fall von κ sind dies das molare Volumen, Vm; die Debye-Temperatur im Hochtemperaturgrenzwert, θD,∞; und die Anharmonizitätsmetrik, σA, wie in Abbildung 1 dargestellt.
Darüber hinaus ermöglicht die beschriebene statistische Analyse, Regeln für die einzelnen Merkmale zu bestimmen, die es erlauben, a priori abzuschätzen, ob ein Material überhaupt ein Wärmeisolator sein kann. Auf diese Weise lassen sich dann hierarchische Entscheidungspyramiden erstellen, mit denen sich die Suche nach neuen Wärmeisolatoren effizient gestalten lässt, wie in Abbildung 2 gezeigt wird. Dabei werden in jedem Schritt die benötigten Materialeigenschaften mit Hilfe von modernsten und genauesten Methoden der Elektronenstrukturtheorie berechnet. Basierend auf den im jeweiligen Schritt berechneten Eigenschaften, werden dann auch Materialien ausgesiebt, bei denen es sehr unwahrscheinlich ist, dass sie gute Isolatoren sind. Damit kann die Anzahl der Berechnungen, die benötigt werden, um Wärmeisolatoren zu finden, um mehr als zwei Größenordnungen reduziert werden. In diesem Fall konnten zum Beispiel 96 Wärmeisolatoren (κ < 10 Wm-1K-1) aus einem anfänglichen Satz von 732 Materialien gefunden werden. Für 4 dieser Vorhersagen wurde anschließend eine hochakkurate Methode angewendet, um κ zu berechnen und die Zuverlässigkeit dieses Ansatzes zu demonstrieren.
Der Nutzen dieses vom NOMAD-Team vorgeschlagenen Formalismus ist nicht auf die aktive Suche nach neuen thermoelektrischen Materialien beschränkt. Er kann ebenso auch auf andere dringliche Probleme der Materialwissenschaft angewendet werden.
Originalveröffentlichung
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
