Das Chaos sichtbar machen
Biophysiker Christian Herbst entwickelt zum 50-jahrigen 'Chaos-Jubilaum' eine neue Visualisierungs-Methode
Exakt 50 Jahre nach der Entdeckung der Chaostheorie durch den US-amerikanischen Mathematiker und Meteorologen Edward Lorenz übt das Thema noch immer eine ungebrochene Faszination aus. Eine neue, an der Universität Wien entwickelte Visualisierungstechnik macht Chaos für das menschliche Auge besser erkennbar. Diese in der Fachzeitschrift "Royal Society Interface" publizierte Methode ermöglicht die einfache Interpretation von chaotischen bzw. chaos-nahen Phänomenen und bringt so die faszinierende Welt der Chaostheorie einer breiteren Öffentlichkeit näher.
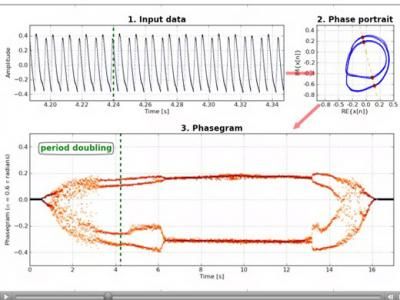
The phase space intersections are then plotted onto a graph at equally spaced time intervals (Fig. 3). The resulting phasegram is quite easy to interpret: Time is on the (horizontal) x-axis. The number and stability of lines perpendicular to the (vertical) y-axis indicates the system state at a particular point in time: one line: no oscillation (stasis) two lines: periodic oscillation four, six, eight etc. lines: period doubling, subharmonic vibrations no continuous lines, rugged appearance: irregular system behavior, indicator for chaos
Christian Herbst
Die Schwingungszustände eines dynamischen (chaotischen) Systems konnten bislang nur durch Verfahren dargestellt werden, welche von Nicht-Mathematikern schwer zu interpretieren sind bzw. mehrere Abbildungen benötigen. Eine Arbeitsgruppe um Biophysiker Christian Herbst vom Department für Kognitionsbiologie der Universität Wien hat nun in Zusammenarbeit mit dem Chaos-Experten Hanspeter Herzel von der Charité in Berlin ein neuartiges Visualisierungsverfahren für derartige Phänomene entwickelt: das sogenannte "Phasegram". Dieses Verfahren erlaubt es, die Symptome von Systemen "auf dem Weg zum Chaos" intuitiv in einer einzigen Abbildung sichtbar zu machen.
Phasegram – die Visualisierungsmethode im Überblick
Chaos ist nicht purer Zufall, sondern kommt durch die Fähigkeit eines simplen Systems, unter bestimmten Rahmenbedingungen komplexes unregelmäßiges Verhalten zu erzeugen, zustande. "Dies trifft auf viele in der Natur vorkommende Phänomene zu: Wetter, Herzrhythmus, Modelle für Bevölkerungswachstum, Wirtschaftsdaten, bestimmte chemische Reaktionen oder die Stimme von Mensch und Tier", erklärt Christian Herbst.
Ein periodisch schwingendes System kann unter bestimmten Umständen durch die minimalste Änderung eines einzigen Einflussfaktors abrupt in chaotisches Verhalten umspringen. Es kann aber auch verschiedene Symptome "auf dem Weg zum Chaos" zeigen: so genannte Periodenverdopplungen bzw. subharmonische Schwingungen, sowie abrupte Sprünge zwischen verschiedenen periodischen Schwingungsarten. Das Schreien von Babys oder das "Kicksen" von Knaben im Stimmbruch sind aus dem Leben gegriffene Beispiele hierfür. "Überhaupt ist die Stimme von Mensch und Tier ein eindrucksvolles und sehr lebensnahes Beispiel eines einfachen dynamischen Systems, welches imstande ist, Chaos zu erzeugen", so Biophysiker Herbst. Daher wird die Phasegram-Methode im Folgenden am Beispiel eines im Labor zur Tonproduktion angeregten Hirsch-Kehlkopfes erläutert.
Zeitsignal
Ausgangspunkt ist ein Zeitsignal, das ist eine in regelmäßigen Abständen von ca. 0,02 ms aufgenommene Reihe von Messdaten, welche die Schwingung der Stimmlippen repräsentiert. Es folgen zwei Verarbeitungsschritte: ein mathematisch relativ komplexer und einer, in welchem das Verhalten des Systems auf einen extrem einfachen Nenner gebracht wird.
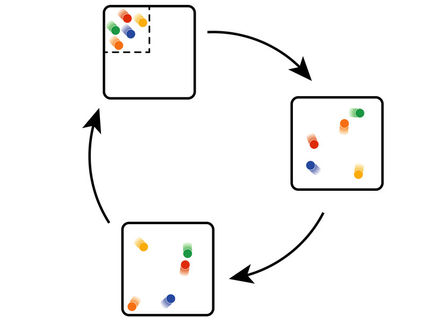
Phasenraum
In regelmäßigen Abständen werden Ausschnitte des oben beschriebenen Zeitsignals in einen so genannten zweidimensionalen Phasenraum eingebettet, und zwar mittels eines vor ca. 30 Jahren beschriebenen mathematischen Verfahrens. Es entsteht eine geometrische Figur, welche je nach Systemverhalten eine distinkte Charakteristik aufweist. Ein Schnitt durch den Phasenraum ergibt die rot gekennzeichneten Schnittpunkte.
Phasegram
Die Schnittpunkte im Phasenraum werden in regelmäßigen Abständen entlang einer Zeitachse aufgetragen. Das resultierende Phasegram ist sehr leicht zu lesen: Zeit verläuft entlang der (horizontalen) x-Achse. Die Anzahl der Linien entlang der (vertikalen) y-Achse lässt auf das Systemverhalten zum jeweiligen Zeitpunkt schließen
- eine Linie: keine Oszillation/Schwingung (Stillstand des Systems)
- zwei Linien: periodische Schwingung
- vier, sechs, acht etc. Linien: Periodenverdopplung, subharmonische Schwingun
- keine durchgängigen Linien: Irreguläres Systemverhalten, Indikator für Chaos
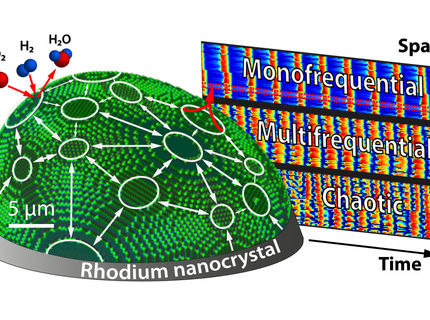
Wie oben erwähnt, zeigt das Phasegram eines im Labor künstlich zur Tonproduktion angeregten Hirschkehlkopfes. Der zum Antrieb der Stimmlippen des Hirsches maßgebliche Luftdruck wurde im Versuchsaufbau als einzige Größe graduell verändert:
Während der ersten Hälfte des Versuches (0 bis 9 Sekunden) steigt der Luftdruck graduell an, danach sinkt er mit gleichbleibender Rate. Der Versuch zeigt auf eindrucksvolle Weise die Fähigkeit eines einfachen Systems, Chaos bzw. Vorstufen dazu zu erzeugen: Trotz der stetigen Veränderung des Luftdrucks ändern sich die gefundenen Schwingungsformen abrupt, die Reihenfolge der durchlaufenen Modi (Stillstand, periodisch, irregulär, Periodenverdopplung, periodisch) ist symmetrisch für zunehmenden bzw. abnehmenden Luftdruck. Das Auftreten der einzelnen Schwingungsformen abhängig vom verwendeten Luftdruck ist im Versuchsaufbau bei gleichbleibenden Rahmenbedingungen verlässlich reproduzierbar.
Originalveröffentlichung
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
