Supercomputer und Quantensimulationen lösen schwieriges Problem der Materialwissenschaft
Japanischen Forschern gelingt es, die Biegeenergie eines Disiloxanmoleküls mit ultrafeinen Molekülsimulationen auf einem Supercomputer zu schätzen
Die strukturellen Eigenschaften von Molekülen, die in der Natur vorkommen oder im Labor synthetisiert werden, zu verstehen, war schon immer das Hauptanliegen von Materialwissenschaftlern. Doch mit den Fortschritten in Wissenschaft und Technik ist das Ziel noch ehrgeiziger geworden: die Entdeckung neuer Materialien mit äußerst wünschenswerten Eigenschaften. Um diese Aufgabe systematisch zu bewältigen, setzen Materialwissenschaftler auf ausgefeilte Simulationstechniken, die die Regeln der Quantenmechanik einbeziehen, dieselben Regeln, die auch die Moleküle selbst steuern.
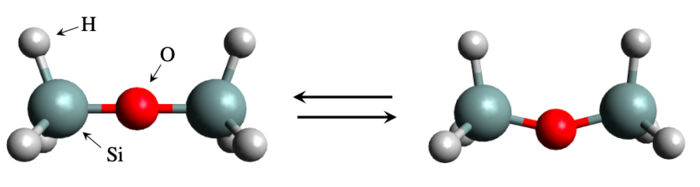
Struktur des Disiloxan-Moleküls in linearer Form (links) und in gebogener Form (rechts). Ein internationales Team von Wissenschaftlern hat die Biegeenergie eines Silikatmoleküls, Disiloxan, untersucht. Obwohl das System einfach und überschaubar zu sein scheint, ist die Berechnung der Biegeenergie mit den herkömmlichen Simulationsmethoden nur schwer zu lösen.
Dr. Kenta Hongo from JAIST
Der simulationsgestützte Ansatz ist so erfolgreich, dass ihm ein ganzes Fachgebiet, die Materialinformatik, gewidmet wurde. Aber es gibt auch Fälle, in denen er scheitert. Ein bemerkenswertes Beispiel ist Disiloxan, eine Silizium (Si)-haltige Verbindung, die aus einer Si-O-Si-Brücke mit drei Wasserstoffatomen an jedem Ende besteht. Die Struktur ist einfach genug, und dennoch ist es bekanntermaßen schwierig, abzuschätzen, wie viel Energie erforderlich ist, um die Si-O-Si-Brücke zu biegen. Die experimentellen Ergebnisse waren widersprüchlich, und die theoretischen Berechnungen ergaben sehr unterschiedliche Werte, da die berechneten Eigenschaften von der Wahl der Parameter und dem Niveau der Theorie abhängen.
Glücklicherweise ist es einem internationalen Forschungsteam unter der Leitung von Dr. Kenta Hongo, außerordentlicher Professor am Japan Advanced Institute of Science and Technology, nun gelungen, dieses Problem zu lösen. In ihrer Studie, die in der Zeitschrift Physical Chemistry Chemical Physics veröffentlicht wurde, gelang dem Team dieses Kunststück durch den Einsatz einer hochmodernen Simulationstechnik, der so genannten "First-Principles-Quantum-Monte-Carlo-Methode", mit der die Schwierigkeiten, die andere Standardtechniken nicht überwinden konnten, endlich überwunden wurden.
Aber läuft das alles nur auf bessere Simulationen hinaus? Nicht ganz. "Eine Antwort zu erhalten, die nicht mit dem experimentell bekannten Wert übereinstimmt, ist an sich nicht überraschend. Die Übereinstimmung kann durch sorgfältigere und teurere Simulationen verbessert werden. Aber bei Disiloxan wird die Übereinstimmung mit sorgfältigeren Simulationen sogar noch schlechter", erklärt Dr. Hongo. "Unsere Methode hat vielmehr gute Ergebnisse ohne große Abhängigkeit von den Anpassungsparametern erzielt, so dass wir uns keine Sorgen machen müssen, ob die angepassten Werte ausreichend sind.
Das Team verglich den First-Principles-Quanten-Monte-Carlo-Ansatz mit anderen Standardtechniken wie Dichtefunktionaltheorie-Berechnungen (DFT) und der "gekoppelten Clustermethode mit einfachen und doppelten Substitutionen und nichtiterativen Tripeln" (CCSD(T)) sowie mit empirischen Messungen aus früheren Studien. Die drei Methoden unterschieden sich hauptsächlich in ihrer Empfindlichkeit gegenüber der "Vollständigkeit" der Basissätze (eine Reihe von Funktionen, die zur Definition der Quantenwellenfunktionen verwendet werden).
Es stellte sich heraus, dass bei DFT und CCSD(T) die Wahl des Basissatzes sowohl die Amplitude als auch die Positionen der Nullamplitude für die Wellenfunktionen beeinflusste, während sie bei Quanten-Monte-Carlo nur die Positionen der Nullamplitude beeinflusste. Auf diese Weise konnte die Amplitude so angepasst werden, dass sich die Form der Wellenfunktion der einer exakten Lösung annäherte. "Diese selbstheilende Eigenschaft der Amplitude funktioniert gut, um die Abhängigkeit vom Basissatz zu reduzieren und die Verzerrung zu verringern, die durch einen unvollständigen Basissatz bei der Berechnung der Biegeenergiebarriere entsteht", erläutert Dr. Hongo.
Während dies an sich schon eine aufregende Entwicklung ist, weist Prof. Hongo auf das größere Bild hin. "Molekulare Simulationen werden in großem Umfang für die Entwicklung neuer Medikamente und Katalysatoren eingesetzt. Die Überwindung der grundlegenden Schwierigkeiten bei ihrer Anwendung trägt wesentlich zur Entwicklung solcher Materialien bei. Mit unseren leistungsstarken Supercomputern könnte die in unserer Studie verwendete Methode eine Standardstrategie zur Überwindung solcher Schwierigkeiten sein", sagt er.
Dies verdient in der Tat die Bezeichnung "Quantensprung"!
Hinweis: Dieser Artikel wurde mit einem Computersystem ohne menschlichen Eingriff übersetzt. LUMITOS bietet diese automatischen Übersetzungen an, um eine größere Bandbreite an aktuellen Nachrichten zu präsentieren. Da dieser Artikel mit automatischer Übersetzung übersetzt wurde, ist es möglich, dass er Fehler im Vokabular, in der Syntax oder in der Grammatik enthält. Den ursprünglichen Artikel in Englisch finden Sie hier.
Originalveröffentlichung
Weitere News aus dem Ressort Wissenschaft
Holen Sie sich die Chemie-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die chemische Industrie, Analytik, Labor und Prozess bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
